Příprava na krátký úvodní kurz stochastického modelování
Pár pojmů (letem-světem, jinak to nejde…)
Diskrétní veličina : nabývá pouze konkrétních hodnot (oka na kostce, počet karet v balíčku, počet oveček v ohradě…)
Spojitá veličina: nekonečně hodnot, plynulá změna (rychlost jízdy, vzdálenost atd.atd.)
Hustota pravděpodobnosti: (Probability Density Function – PDF) funkce, jejíž integrací na kterémkoliv vzorku/podmnožině získáme relativní pravděpodobnost, že hodnota náhodné proměnné by se rovnala tomuto vzorku.
Je to trochu kostrbaté, ale je to tak.
Integrace funkce PDF přes celou definiční oblast
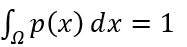
a pravděpodobnost, že jev v určitém intervalu hodnot nastane pak:
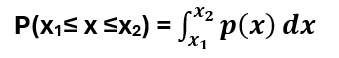
Zcela minimalistický úvod do integrálního počtu (jedné proměnné)
Integrací se nazývá nalezení tzv. primitivní funkce, jde v podstatě o proces opačný k derivaci funkce.
Ne vždy lze primitivní funkci nalézt matematickými metodami, integrace je pak prováděna zejména numerickými metodami (v případě potřeby výpočtu hodnoty určitého integrálu tj. na konkrétním intervalu „od-do“)
Např. víme (z teorie diferenciálního počtu), že derivace funkce x3 (dle x, jak jinak) je rovno 3x2
Budeme-li tedy integrovat funkci x2 –tedy
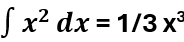
(+ libovolná konstanta, neboť derivace konstanty je nula) – a to je právě ona „primitivní funkce“.
Jinak tedy:
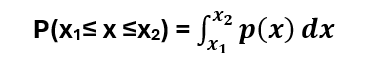
Pro matematická řešení integrálů složitějších funkcí jsou dále užívány nejrůznější metody, nejznámější a nejpoužívanější jsou metoda substituční a metoda per partes (=po částech)
Více příslušná literatura.
Dále lze např. okrajově zmínit, že přímočarý rovnoměrný pohyb (těles, hmotného bodu) tj. objekt pohybující se konstantní rychlostí v urazí za čas t dráhu =v*t
Dráha je matematicky vzato integrálem rychlosti dle času tedy
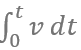
přičemž v je zde konstantou a integrál dt = t , tedy s= v*t
Začneme–li ještě k tomu nějak pracovat s pohybem zrychleným či zpomaleným (pro zjednodušení se zrychlením/zpomalením konstantním) pak integrálem zrychlení je rychlost a další integrací pak dráha.
Integrujeme zde již rychlost rovnoměrně zrychleného pohybu (= a*t) podle času t
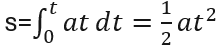
Z toho je již asi jasnější , kde se v tomto vztahu vzala ta ½ a ona druhá mocnina času.
Nejdůležitější druhy rozdělení
Pomineme zcela rozdělení diskrétních veličin, tedy nebudeme házet kostkou či mincemi a vrhneme se rovnou na dvě nejdůležitější rozdělení veličin spojitých, (které mají či to s optimizmem nám vlastním alespoň předpokládáme) nejrozšířenější využití v praktické stochastické analýze dějů, jako je např. nehodová analýza.
Rozdělení ROVNOMĚRNÉ
Zde je pravděpodobnost, že veličina nabývá určité hodnoty je shodná, stejná na celém námi definovaném intervalu možných hodnot.
Hustota (pravděpodobnosti) rovnoměrného rozdělení
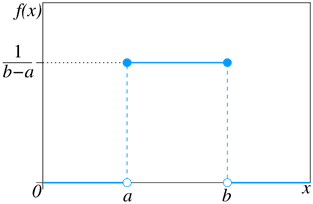
Distribuční funkce rovnoměrného rozdělení
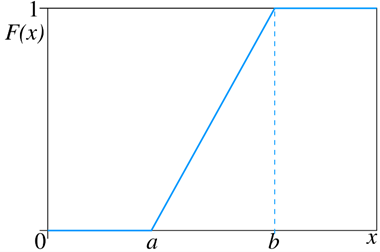
Pokud si nebudeme zcela jisti, zda konkrétní veličina má skutečně rozdělení rovnoměrné, jeho „nasazením“ pak velkou chybu neuděláme, neboť je tu ještě „berlička v podobě „centrální limitní věty“ – součet nebo průměr velkého počtu nezávislých náhodných veličin má (za určitých podmínek) přibližně normální rozdělení (Gaussovo rozdělení), bez ohledu na původní rozdělení těchto veličin.
A tak jsme se nenásilně posunuli rovnou ke „Svatému Grálu statistiky“ kterým je rozdělení NORMÁLNÍ neboli Gaussovo popř. Gauss-Laplaceovo
Klíčové vlastnosti (tyto jsou zcela sprostě opsány z internetu, protože už opravdu nelze vymyslet dokonalejší formulace)
- Tvar: Má symetrický zvonovitý tvar, kde vrchol je nad střední hodnotou (μ).
- Parametry: Určeno střední hodnotou (μ, určuje polohu) a rozptylem (σ², určuje šířku křivky).
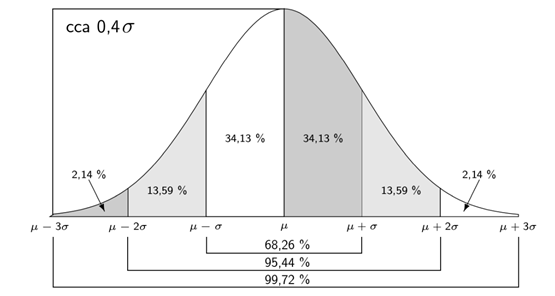
- Pravděpodobnost: Hodnoty blízké střední hodnotě jsou nejpravděpodobnější.Pravidlo tří sigma říká, že 99,7 % hodnot leží v intervalu (μ-3σ, μ+3σ).
- Všudypřítomnost: Modeluje jevy ovlivněné mnoha malými, nezávislými faktory (např. chyby měření, IQ, výšky), proto se mu říká i zákon chyb.
V technické praxi nebudeme dogmaticky trvat na „třech sigmách“, zcela postačující bude oblast pravděpodobnosti ±2σ což je cca 95 % a tento rozsah je označován u soudů v anglosaských zemích jako nade vší pochybnost
Jak často uvádím, naše soudy a obecně vše kolem nás co je ovládáno a řízeno všeobjímajícím laskavým státem jsou vždy „papežštější než papež“ a proto lze vřele doporučit vše „posichrovat“ na ±2,5 σ = TECHNICKÁ JISTOTA s pravděpodobností 99 %.
Tuto už by nejspíš nemusel zuřivě napadat ani ten nejchytřejší z nejchytřejších advokátních koncipientů.
Hustota pravděpodobnosti normálního rozdělení
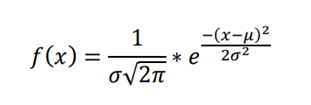
Strašlivý vzorec, který si jen málokdo pamatuje.
Čísla x a µ jsou reálná, konstanta σ nabývá kladné hodnoty.
Konstanta µ značí střední hodnotu náhodné veličiny X.
Konstanta σ značí směrodatnou odchylku náhodné veličiny, která po umocnění je rozptyl normálního rozdělení.
Parametr µ určuje maximum křivky.
Parametr σ určuje vzdálenost inflexních bodů od hodnoty µ
Křivka je zvonovitého tvaru a je symetrická kolem µ.
Distribuční funkce
Primitivní funkci k funkci hustoty pravděpodobnosti normálního rozdělení nelze jednoduše „exaktně“ určit, numerické řešení průběhu distribuční funkce je samozřejmě možné.
Integrál hustoty pravděpodobnosti na intervalu (-∞; ∞) je pochopitelně rovný 1
Průběh distribuční funkce pro různé hodnoty σ:
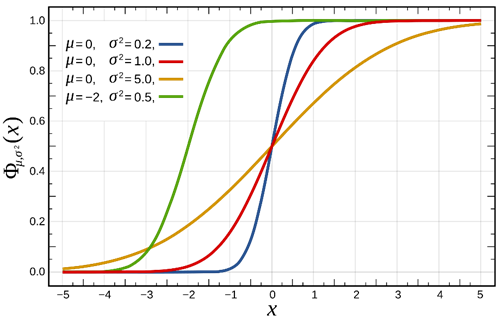
Červeně je vyznačeno tzv. „normované“ Gaussovo rozdělení kde µ=0 a σ = 1
Pomocí něj lze z univerzálních, „tabulkových“ hodnot normálního normovaného rozdělení přejít snadno na jiné parametry µ a σ.
Zkuste dosavadní uvedené poznatky třeba nějak „pochroupat“, literatury je k dispozici i volně na internetu doslova „neúrekom“.
K základnímu objasnění integrálního počtu např.
https://cs.khanacademy.org/math/integralni-pocet/xbf9b4d9711003f1c:aplikace-integralu/xbf9b4d9711003f1c:obsah-utvaru/v/evaluating-simple-definite-integral
Příště si už snad konečně dáme tu Buffonovu jehlu a Monte Carlo v MS Excel
